LECCION 36: "Teorema Central del Límite: Ejercicios (I)"

EJEMPLO 1

OTROS EJEMPLOS

LECCION 35: "Teorema Central del Límite"

El Teorema Central del Límite dice que si tenemos un grupo numeroso de variables independientes y todas ellas siguen el mismo modelo de distribución (cualquiera que éste sea), la suma de ellas se distribuye según una distribución normal.

EJEMPLO: la variable "tirar una moneda al aire" sigue la distribución de Bernouilli. Si lanzamos la moneda al aire 50 veces, la suma de estas 50 variables (cada una independiente entre si) se distribuye según una distribución normal.

Este teorema se aplica tanto a suma de variables discretas como de variables continuas.

Los parámetros de la distribución normal son:

1. Media: n * m (media de la variable individual multiplicada por el número de variables independientes)
2. Varianza: n * s2 (varianza de la variable individual multiplicada por el número de variables individuales)

LECCION 34: "Distribuciones continuas: Normal (III): Ejercicios "

A continuación se plantean ejercios resueltos para una mejor comprensión de la distribución normal:

LECCION 33: "Distribuciones continuas: Normal (II)"

La distribución normal tipificada tiene la ventaja, como ya hemos indicado, de que las probabilidades para cada valor de la curva se encuentran recogidas en una tabla.

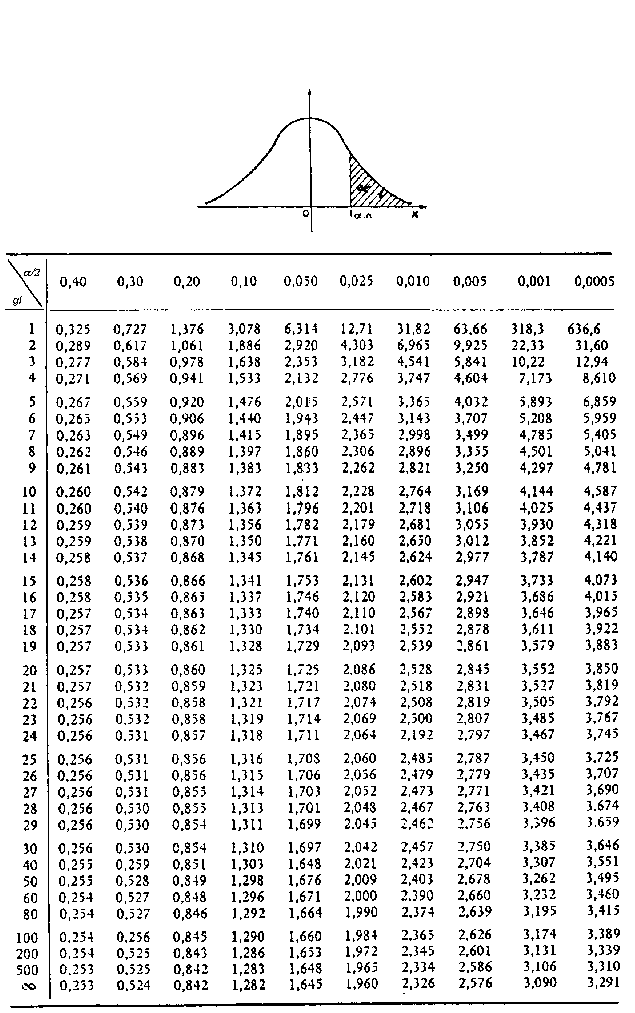
¿Cómo se lee esta tabla?
La columna de la izquierda indica el valor cuya probabilidad acumulada queremos conocer. La primera fila nos indica el segundo decimal del valor que estamos consultando.

EJEMPLO: queremos conocer la probabilidad acumulada en el valor 2,75.Entonces buscamos en la columna de la izquierda el valor 2,7 y en la primera fila el valor 0,05. La casilla en la que se interseccionan es su probabilidad acumulada (0,99702, es decir 99.7%).

Atención: la tabla nos da la probabilidad acumulada, es decir, la que va desde el inicio de la curva por la izquierda hasta dicho valor. No nos da la probabilidad concreta en ese punto. En una distribución continua en el que la variable puede tomar infinitos valores, la probabilidad en un punto concreto es prácticamente despreciable.

LECCION 32: "Distribuciones continuas: Normal (I)"

Es el modelo de distribución más utilizado en la práctica, ya que multitud de fenómenos se comportan según una distribución normal.

Esta distribución de caracteriza porque los valores se distribuyen formando una campana de Gauss, en torno a un valor central que coincide con el valor medio de la distribución:

Un 50% de los valores están a la dercha de este valor central y otro 50% a la izquierda

Esta distribución viene definida por dos parámetros:

X: N (m, s 2)

m : es el valor medio de la distribución y es precisamente donde se sitúa el centro de la curva (de la campana de Gauss).

s 2 : es la varianza. Indica si los valores están más o menos alejados del valor central: si la varianza es baja los valores están próximos a la media; si es alta, entonces los valores están muy dispersos.

Cuando la media de la distribución es 0 y la varianza es 1se denomina "normal tipificada", y su ventaja reside en que hay tablas donde se recoge la probabilidad acumulada para cada punto de la curva de esta distribución.

Además, toda distribución normal se puede transformar en una normal tipificada:

EJEMPLO: una variable aleatoria sigue el modelo de una distribución normal con media 10 y varianza 4. Transformarla en una normal tipificada.

X: N (10, 4)

Para transformarla en una normal tipificada se crea una nueva variable (Y) que será igual a la anterior (X) menos su media y dividida por su desviación típica (que es la raíz cuadrada de la varianza)

Esta nueva variable se distribuye como una normal tipificada, permitiéndonos, por tanto, conocer la probabilidad acumulada en cada valor.

LECCION 31: "Distribuciones continuas: Uniforme "

La distribución uniforme es aquella que puede tomar cualquier valor dentro de un intervalo, todos ellos con la misma probabilidad.

Es una distribución continua porque puede tomar cualquier valor y no únicamente un número determinado (como ocurre en las distribuciones discretas).

EJEMPLO: el precio medio del litro de gasolina durante el próximo año se estima que puede oscilar entre 140 y 160 ptas. Podría ser, por tanto, de 143 ptas., o de 143,4 ptas., o de 143,45 ptas., o de 143,455 ptas, etc. Hay infinitas posibilidades, todas ellas con la misma probabilidad.

Su función de densidad, aquella que nos permite conocer la probabilidad que tiene cada punto del intervalo, viene definida por:

Donde:

b: es el extremo superior (en el ejemplo, 160 ptas.)

a: es el extremo inferior (en el ejemplo, 140 ptas.)

EJEMPLO

LECCION 30: "Distribuciones Discretas: Multihipergeométrica"

La distribución multihipergeométrica es similar a la distribución hipergeométrica, con la diferencia de que en la urna, en lugar de haber únicamente bolas de dos colores, hay bolas de diferentes colores.

EJEMPLO: en una urna hay 7 bolas blancas, 3 verdes y 4 amarillas: ¿cuál es la probabilidad de que al extraer 3 bolas sea cada una de un color distinto?

La distribución multihipergeométrica sigue el siguiente modelo:

Donde:

X1 = x1: indica que el suceso X1 aparezca x1 veces (en el ejemplo, que una de las bolas sea blanca)

N1: indica el número de bolas blancas que hay en la urna (en el ejemplo, 7 bolas)

N: es el número total de bolas en la urna (en el ejemplo, 14 bolas)

n: es el número total de bolas que se extraen (en el ejemplo, 3 bolas)

EJEMPLO

Luego:

P = 0,2307

Es decir, que la probabilidad de sacar una bola de cada color es del 23,07%.