LECCION 36: "Teorema Central del Límite: Ejercicios (I)"

EJEMPLO 1

OTROS EJEMPLOS

LECCION 35: "Teorema Central del Límite"

El Teorema Central del Límite dice que si tenemos un grupo numeroso de variables independientes y todas ellas siguen el mismo modelo de distribución (cualquiera que éste sea), la suma de ellas se distribuye según una distribución normal.

EJEMPLO: la variable "tirar una moneda al aire" sigue la distribución de Bernouilli. Si lanzamos la moneda al aire 50 veces, la suma de estas 50 variables (cada una independiente entre si) se distribuye según una distribución normal.

Este teorema se aplica tanto a suma de variables discretas como de variables continuas.

Los parámetros de la distribución normal son:

1. Media: n * m (media de la variable individual multiplicada por el número de variables independientes)
2. Varianza: n * s2 (varianza de la variable individual multiplicada por el número de variables individuales)

LECCION 34: "Distribuciones continuas: Normal (III): Ejercicios "

A continuación se plantean ejercios resueltos para una mejor comprensión de la distribución normal:

LECCION 33: "Distribuciones continuas: Normal (II)"

La distribución normal tipificada tiene la ventaja, como ya hemos indicado, de que las probabilidades para cada valor de la curva se encuentran recogidas en una tabla.

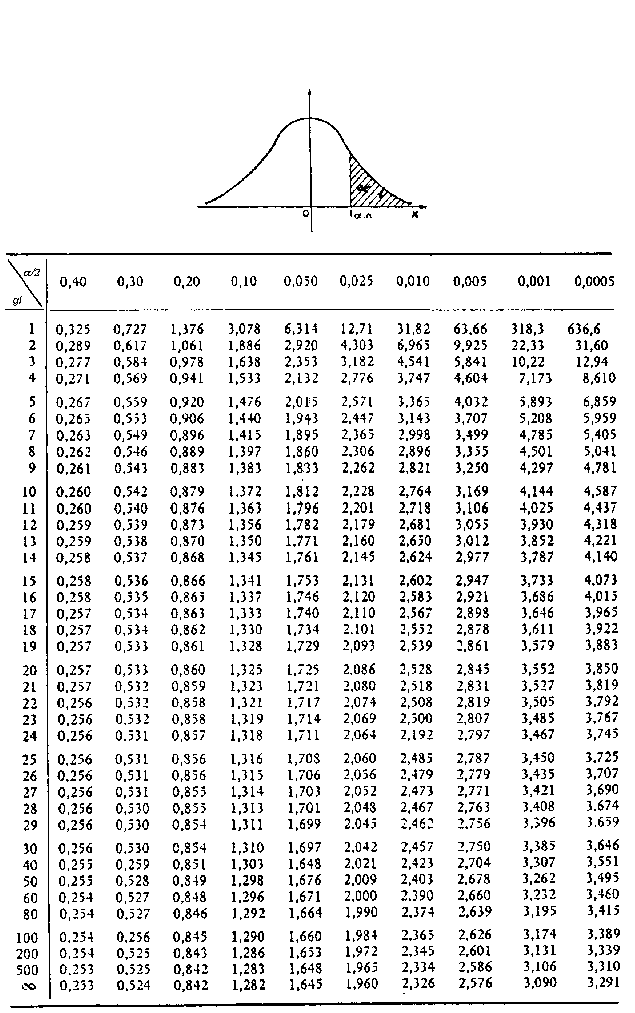
¿Cómo se lee esta tabla?
La columna de la izquierda indica el valor cuya probabilidad acumulada queremos conocer. La primera fila nos indica el segundo decimal del valor que estamos consultando.

EJEMPLO: queremos conocer la probabilidad acumulada en el valor 2,75.Entonces buscamos en la columna de la izquierda el valor 2,7 y en la primera fila el valor 0,05. La casilla en la que se interseccionan es su probabilidad acumulada (0,99702, es decir 99.7%).

Atención: la tabla nos da la probabilidad acumulada, es decir, la que va desde el inicio de la curva por la izquierda hasta dicho valor. No nos da la probabilidad concreta en ese punto. En una distribución continua en el que la variable puede tomar infinitos valores, la probabilidad en un punto concreto es prácticamente despreciable.

LECCION 32: "Distribuciones continuas: Normal (I)"

Es el modelo de distribución más utilizado en la práctica, ya que multitud de fenómenos se comportan según una distribución normal.

Esta distribución de caracteriza porque los valores se distribuyen formando una campana de Gauss, en torno a un valor central que coincide con el valor medio de la distribución:

Un 50% de los valores están a la dercha de este valor central y otro 50% a la izquierda

Esta distribución viene definida por dos parámetros:

X: N (m, s 2)

m : es el valor medio de la distribución y es precisamente donde se sitúa el centro de la curva (de la campana de Gauss).

s 2 : es la varianza. Indica si los valores están más o menos alejados del valor central: si la varianza es baja los valores están próximos a la media; si es alta, entonces los valores están muy dispersos.

Cuando la media de la distribución es 0 y la varianza es 1se denomina "normal tipificada", y su ventaja reside en que hay tablas donde se recoge la probabilidad acumulada para cada punto de la curva de esta distribución.

Además, toda distribución normal se puede transformar en una normal tipificada:

EJEMPLO: una variable aleatoria sigue el modelo de una distribución normal con media 10 y varianza 4. Transformarla en una normal tipificada.

X: N (10, 4)

Para transformarla en una normal tipificada se crea una nueva variable (Y) que será igual a la anterior (X) menos su media y dividida por su desviación típica (que es la raíz cuadrada de la varianza)

Esta nueva variable se distribuye como una normal tipificada, permitiéndonos, por tanto, conocer la probabilidad acumulada en cada valor.

LECCION 31: "Distribuciones continuas: Uniforme "

La distribución uniforme es aquella que puede tomar cualquier valor dentro de un intervalo, todos ellos con la misma probabilidad.

Es una distribución continua porque puede tomar cualquier valor y no únicamente un número determinado (como ocurre en las distribuciones discretas).

EJEMPLO: el precio medio del litro de gasolina durante el próximo año se estima que puede oscilar entre 140 y 160 ptas. Podría ser, por tanto, de 143 ptas., o de 143,4 ptas., o de 143,45 ptas., o de 143,455 ptas, etc. Hay infinitas posibilidades, todas ellas con la misma probabilidad.

Su función de densidad, aquella que nos permite conocer la probabilidad que tiene cada punto del intervalo, viene definida por:

Donde:

b: es el extremo superior (en el ejemplo, 160 ptas.)

a: es el extremo inferior (en el ejemplo, 140 ptas.)

EJEMPLO

LECCION 30: "Distribuciones Discretas: Multihipergeométrica"

La distribución multihipergeométrica es similar a la distribución hipergeométrica, con la diferencia de que en la urna, en lugar de haber únicamente bolas de dos colores, hay bolas de diferentes colores.

EJEMPLO: en una urna hay 7 bolas blancas, 3 verdes y 4 amarillas: ¿cuál es la probabilidad de que al extraer 3 bolas sea cada una de un color distinto?

La distribución multihipergeométrica sigue el siguiente modelo:

Donde:

X1 = x1: indica que el suceso X1 aparezca x1 veces (en el ejemplo, que una de las bolas sea blanca)

N1: indica el número de bolas blancas que hay en la urna (en el ejemplo, 7 bolas)

N: es el número total de bolas en la urna (en el ejemplo, 14 bolas)

n: es el número total de bolas que se extraen (en el ejemplo, 3 bolas)

EJEMPLO

Luego:

P = 0,2307

Es decir, que la probabilidad de sacar una bola de cada color es del 23,07%.

LECCION 29: "Distribuciones Discretas: Multinomial "

La distribución multinomial es similar a la distribución binomial, con la diferencia de que en lugar de dos posibles resultados en cada ensayo, puede haber múltiples resultados:

Ejemplo de distribución binomial:

a unas elecciones se presentaron 2 partidos políticos: el POPO obtuvo un 70% de los votos y el JEJE el 30% restante. ¿Cuál es la probabilidad de que al elegir 5 ciudadanos al azar, 4 de ellos hallan votado al JEJE?

Ejemplo de distribución multinomial:

a esas elecciones se presentaron 4 partidos políticos: el POPO obtuvo un 40% de los votos, el JEJE el 30%, el MUMU el 20% y el LALA el 10% restante. ¿Cuál es la probabilidad de que al elegir 5 ciudadanos al azar, 3 hayan votado al POPO, 1 al MUMU y 1 al LALA?

La distribución multinomial sigue el siguiente modelo:

Donde:

X1 = x1: indica que el suceso X1 aparezca x1 veces (en el ejemplo, que el partido POPO lo hayan votado 3 personas)

n: indica el número de veces que se ha repetido el suceso (en el ejemplo, 5 veces)

n!: es factorial de n (en el ejemplo: 5 * 4 * 3 * 2 * 1)

p1: es la probabilidad del suceso X1 (en el ejemplo, el 40%)

LECCION 28: "Distribuciones Discretas: Hipergeométrica "

Las distribución hipergeométrica es el modelo que se aplica en experimentos del siguiente tipo:

En una urna hay bolas de dos colores (blancas y negras), ¿cuál es la probabilidad de que al sacar 2 bolas las dos sean blancas?

Son experimentos donde, al igual que en la distribución binomial, en cada ensayo hay tan sólo dos posibles resultados: o sale blanca o no sale. Pero se diferencia de la distribución binomial en que los distintos ensayos son dependientes entre sí:

Si en una urna con 5 bolas blancas y 3 negras en un primer ensayo saco una bola blanca, en el segundo ensayo hay una bola blanca menos por lo que las probabilidades son diferentes (hay dependencia entre los distintos ensayos).

La distribución hipergeométrica sigue el siguiente modelo:

EN DONDE:

Vamos a tratar de explicarlo:

N: es el número total de bolas en la urna

N1: es el número total de bolas blancas

N2: es el número total de bolas negras

k: es el número de bolas blancas cuya probabilidad se está calculando

n: es el número de ensayos que se realiza

LECCION 27: "Distribuciones Discretas: Poisson"

Las distribución de Poisson parte de la distribución binomial:
Cuando en una distribución binomial se realiza el experimento un número "n" muy elevado de veces y la probabilidad de éxito "p" en cada ensayo es reducida, entonces se aplica el modelo de distribución de Poisson:
Se tiene que cumplir que:
" p " < 0,10
" p * n " < 10
La distribución de Poisson sigue el siguiente modelo:

Vamos a explicarla:

El número "e" es 2,71828
" l " = n * p (es decir, el número de veces " n " que se realiza el experimento multiplicado por la probabilidad " p " de éxito en cada ensayo)
" k " es el número de éxito cuya probabilidad se está calculando

LECCION 26: "Distribuciones Discretas: Binomial"

Las distribución binomial parte de la distribución de Bernouilli:

La distribución de Bernouiili se aplica cuando se realiza una sola vez un experimento que tiene únicamente dos posibles resultados (éxito o fracaso), por lo que la variable sólo puede tomar dos valores: el 1 y el 0

La distribución binomial se aplica cuando se realizan un número"n" de veces el experimento de Bernouiili, siendo cada ensayo independiente del anterior. La variable puede tomar valores entre:

0: si todos los experimentos han sido fracaso

n: si todos los experimentos han sido éxitos

EJEMPLO: se tira una moneda 10 veces: ¿cuantas caras salen? Si no ha salido ninguna la variable toma el valor 0; si han salido dos caras la variable toma el valor 2; si todas han sido cara la variable toma el valor 10

La distribución de probabilidad de este tipo de distribución sigue el siguiente modelo:

Ampliemos un poco más el tema...

LECCION 25: "Distribuciones Discretas: Bernouilli"

Es aquel modelo que sigue un experimento que se realiza una sola vez y que puede tener dos soluciones: acierto o fracaso:

Cuando es acierto la variable toma el valor 1

Cuando es fracaso la variable toma el valor 0

EJEMPLO: Probabilidad de salir cara al lanzar una moneda al aire (sale cara o no sale); probabilidad de ser admitido en una universidad (o te admiten o no te admiten); probabilidad de acertar una quiniela (o aciertas o no aciertas)

Al haber únicamente dos soluciones se trata de sucesos complementarios:

A la probabilidad de éxito se le denomina "p"

A la probabilidad de fracaso se le denomina "q"

Verificándose que:

p + q = 1

LECCION 24: "Distribuciones Discretas y Continuas"

Podemos encontrar dos tipos de distribuciones, las cuales son:

1. DISTRIBUCIONES DISCRETAS
   son aquellas en las que la variable puede pude tomar un número determinado de valores:
   

   EJEMPLO: si se lanza una moneda al aire puede salir cara o cruz; si se tira un dado puede salir un número de 1 al 6; en una ruleta el número puede tomar un valor del 1 al 32.

2. DISTRIBUCIONES CONTINUAS
   son aquellas que presentan un número infinito de posibles soluciones:
   

   EJEMPLO: el peso medio de los alumnos de una clase puede tomar infinitos valores dentro de cierto intervalo (42,37 kg, 42,3764 kg, 42, 376541kg, etc); la esperanza media de vida de una población (72,5 años, 7,513 años, 72, 51234 años).

   
   

LECCION 23: "Independencia de Sucesos"

Dos sucesos son independientes entre sí, si la ocurrencia de uno de ellos no afecta para nada a la ocurrencia del otro:
Para que dos sucesos sean independientes tienen que verificar al menos una de las siguientes condiciones:

P (B/A) = P (B)

es decir, que la probabilidad de que se de el suceso B, condicionada a que previamente se haya dado el suceso A, es exactamente igual a la probabilidad de B.

P (A/B) = P (A)

es decir, que la probabilidad de que se de el suceso A, condicionada a que previamente se haya dado el suceso B, es exactamente igual a la probabilidad de A.

P (A L B) = P (A) * P (B)

es decir, que la probabilidad de que se de el suceso conjunto A y B es exactamente igual a la probabilidad del suceso A multiplicada por la probabilidsad del suceso B.

Si el suceso A es independiente del suceso B, entonces el suceso B también es independiente del suceso A.

LECCION 22: "Teorema de Bayes "

El Teorema de Bayes viene a seguir el proceso inverso al que hemos visto en el Teorema de la probabilidad total:

Teorema de la probabilidad total:

a partir de las probabilidades del suceso A (probabilidad de que llueva o de que haga buen tiempo) deducimos la probabilidad del suceso B (que ocurra un accidente).

Teorema de Bayes:

a partir de que ha ocurrido el suceso B (ha ocurrido un accidente) deducimos las probabilidades del suceso A (¿estaba lloviendo o hacía buen tiempo?).

La fórmula del Teorema de Bayes es:

Tratar de explicar estar fórmula con palabras es un galimatías, así que vamos a intentar explicarla con un ejemplo. De todos modos, antes de entrar en el ejercicio, recordar que este teorema también exige que el suceso A forme un sistema completo.

EJEMPLO

LECCION 21: "Teorema de la Probabilidad Total "

El Teorema de la probabilidad total nos permite calcular la probabilidad de un suceso a partir de probabilidades condicionadas:

EJEMPLO: supongamos que si llueve la probabilidad de que ocurra un accidentes es x% y si hace buen tiempo dicha probabilidad es y%. Este teorema nos permite deducir cuál es la probabilidad de que ocurra un accidente si conocemos la probabilidad de que llueva y la probabilidad de que haga buen tiempo.

La fórmula para calcular esta probabilidad es:

Es decir, la probabilidad de que ocurra el suceso B (en nuestro ejemplo, que ocurra un accidente) es igual a la suma de multiplicar cada una de las probabilidades condicionadasde este suceso con los diferentes sucesos A (probabilidad de un accidente cuando llueve y cuando hace buen tiempo) por la probabilidad de cada suceso A.
Para que este teorema se pueda aplicar hace falta cumplir un requisito:
Los sucesos A tienen que formar un sistema completo, es decir, que contemplen todas las posibilidades (la suma de sus probabilidades debe ser el 100%).

LECCION 20: "Probabilidad Compuesta"

La probabilidad compuesta (o regla de multiplicación de probabilidades) se deriva de la probabilidad condicionada:

La probabilidad de que se den simultáneamente dos sucesos (suceso intersección de A y B) es igual a la probabilidad a priori del suceso A multiplicada por la probabilidad del suceso B condicionada al cumplimiento del suceso A.

LECCION 19: "Probabilidad Condicionada"

Las probabilidades condicionadas se calculan una vez que se ha incorporado información adicional a la situación de partida.

Las probabilidades condicionadas se calculan aplicando la siguiente fórmula:

Donde:

P (B/A)

es la probabilidad de que se de el suceso B condicionada a que se haya dado el suceso A.

P (B L A)

es la probabilidad del suceso simultáneo de A y de B

P (A)

Definicion 2es la probabilidad a priori del suceso A

EJEMPLOS: "Combinaciones, Variaciones y Permutaciones"

EJEMPLOS 1:

EJEMPLO 2:

EJEMPLO 3:

LECCION 18: "Combinaciones, Variaciones y Permutaciones (III)"

FORMULAS COMBINACIONES

Definición de fórmulas de combinaciones con y sin repetición:

FORMULAS VARIACIONES

Definición de fórmulas de variaciones con y sin repetición:

FORMULAS PERMUTACIONES

Definición de fórmulas de permutaciones con y sin repetición:

LECCION 17: "Combinaciones, Variaciones y Permutaciones (II)"

¿COMO SE CALCULAN?

1. COMBINACIONES
   Para calcular el número de combinaciones se aplica la siguiente fórmula:
   
   
   El termino " n ! " se denomina "factorial de n" y es la multiplicación de todos los números que van desde "n" hasta 1.
   

   Ejemplo: C10,4 son las combinaciones de 10 elementos agrupándolos en subgrupos de 4 elementos: Es decir, podríamos formar 210 subgrupos diferentes de 4 elementos, a partir de los 10 elementos.



2. VARIACIONES
   Para calcular el número de variaciones se aplica la siguiente fórmula:
   
   
   La expresión "Vm,n" representa las variaciones de "m" elementos, formando subgrupos de "n" elementos. En este caso, como vimos en la lección anterior, un subgrupo se diferenciará del resto, bien por los elementos que lo forman, o bien por el orden de dichos elementos.
   

   Ejemplo: V10,4 son las variaciones de 10 elementos agrupándolos en subgrupos de 4 elementos: Es decir, podríamos formar 5.040 subgrupos diferentes de 4 elementos, a partir de los 10 elementos.



3. PERMUTACIONES
   Para calcular el número de permutaciones se aplica la siguiente fórmula:
   
   
   La expresión "Pm" representa las permutaciones de "m" elementos, tomando todos los elementos. Los subgrupos se diferenciaran únicamente por el orden de los elementos.
   

   Ejemplo: P10 son las permutaciones de 10 elementos: Es decir, tendríamos 3.628.800 formas diferentes de agrupar 10 elementos.

LECCION 16: "Combinaciones, Variaciones y Permutaciones (I)"

Para aplicar la Regla de Laplace el cálculo de los sucesos favorables y de los sucesos posibles a veces no plantea ningún problema, ya que son un número reducido y se pueden calcular con facilidad.

Sin embargo, a veces calcular el número de casos favorables y casos posibles es complejo y hay que aplicar reglas matemáticas:

Por ejemplo: 5 matrimonios se sientan aleatoriamente a cenar y queremos calcular la probabilidad de que al menos los miembros de un matrimonio se sienten junto. En este caso, determinar el número de casos favorables y de casos posibles es complejo.

Las reglas matemáticas que nos pueden ayudar son el cálculo de combinaciones, el cálculo devariaciones y el cálculo de permutaciones.

1. COMBINACIONES: Determina el número de subgrupos de 1, 2, 3, etc. elementos que se pueden formar con los "n" elementos de una nuestra. Cada subgrupo se diferencia del resto en los elementos que lo componen, sin que influya el orden.

   EJEMPLO, calcular las posibles combinaciones de 2 elementos que se pueden formar con los números 1, 2 y 3. Se pueden establecer 3 parejas diferentes: (1,2), (1,3) y (2,3). En el cálculo de combinaciones las parejas (1,2) y (2,1) se consideran idénticas, por lo que sólo se cuentan una vez.

2. VARIACIONES: Calcula el número de subgrupos de 1, 2, 3, etc.elementos que se pueden establecer con los "n" elementos de una muestra. Cada subgrupo se diferencia del resto en los elementos que lo componen o en el orden de dichos elementos (es lo que le diferencia de las combinaciones).

   EJEMPLO, calcular las posibles variaciones de 2 elementos que se pueden establecer con los número 1, 2 y 3. Ahora tendríamos 6 posibles parejas: (1,2), (1,3), (2,1), (2,3), (3,1) y (3,3). En este caso los subgrupos (1,2) y (2,1) se consideran distintos.

3. PERMUTACIONES: Cálcula las posibles agrupaciones que se pueden establecer con todos los elementos de un grupo, por lo tanto, lo que diferencia a cada subgrupo del resto es el orden de los elementos.

   EJEMPLO, calcular las posibles formas en que se pueden ordenar los número 1, 2 y 3. Hay 6 posibles agrupaciones: (1, 2, 3), (1, 3, 2), (2, 1, 3), (2, 3, 1), (3, 1, 2) y (3, 2, 1).

EJEMPLOS Y EJERCICIOS: "Probabilidad"

EJEMPLO 1

EJEMPLO 2

EJERCICIOS PARA REPASO

LECCION 15: "Cálculo de probabilidades"

Como hemos comentado anteriormente, la probabilidad mide la mayor o menor posibilidad de que se dé un determinado resultado (suceso) cuando se realiza un experimento aleatorio.
La probabilidad toma valores entre 0 y 1 (o expresados en tanto por ciento, entre 0% y 100%):

El valor cero corresponde al suceso imposible:

lanzamos un dado al aire y la probabilidad de que salga el número 7 es cero (al menos, si es un dado certificado por la OMD, "Organización Mundial de Dados").

El valor uno corresponde al suceso seguro:

lanzamos un dado al aire y la probabilidad de que salga cualquier número del 1 al 6 es igual a uno (100%).

El resto de sucesos tendrá probabilidades entre cero y uno:

que será tanto mayor cuanto más probable sea que dicho suceso tenga lugar.

¿Cómo se mide la probabilidad?
Uno de los métodos más utilizados es aplicando la Regla de Laplace: define la probabilidad de un suceso como el cociente entre casos favorables y casos posibles.
P(A) = Casos favorables / casos posibles

EJEMPLOS

Probabilidad de que al lanzar un dado salga el número 2:el caso favorable es tan sólo uno (que salga el dos), mientras que los casos posibles son seis (puede salir cualquier número del uno al seis). Por lo tanto: P(A) = 1 / 6 = 0,166 (o lo que es lo mismo, 16,6%)
Probabilidad de que al lanzar un dado salga un número par:en este caso los casos favorables son tres (que salga el dos, el cuatro o el seis), mientras que los casos posibles siguen siendo seis. Por lo tanto: P(A) = 3 / 6 = 0,50 (o lo que es lo mismo, 50%)

PROPIEDADES DE LA PROBABILIDAD (parte 1)

PROPIEDADES DE LA PROBABILIDAD (parte 2)

LECCION 14: "Probabilidad: Relación Entre Sucesos"

Entre los sucesos compuestos se pueden establecer distintas relaciones:

1. Un suceso puede estar contenido en otro: las posibles soluciones del primer suceso también lo son del segundo, pero este segundo suceso tiene además otras soluciones suyas propias.


2. Dos sucesos pueden ser iguales: esto ocurre cuando siempre que se cumple uno de ellos se cumple obligatoriamente el otro y viceversa.


3. Unión de dos o más sucesos: la unión será otro suceso formado por todos los elementos de los sucesos que se unen.


4. Intersección de sucesos: es aquel suceso compuesto por los elementos comunes de dos o más sucesos que se intersectan.


5. Sucesos incompatibles: son aquellos que no se pueden dar al mismo tiempo ya que no tienen elementos comunes (su interesección es el conjunto vacio).


6. Sucesos complementarios: son aquellos que si no se da uno, obligatoriamente se tiene que dar el otro.

LECCION 13: "Probabilidad: Introducción"

La probabilidad mide la frecuencia con la que aparece un resultado determinado cuando se realiza un experimento.

EJEMPLO: tiramos un dado al aire y queremos saber cual es la probabilidad de que salga un 2, o que salga un número par, o que salga un número menor que 4.

El experimento tiene que ser aleatorio, es decir, que pueden presentarse diversos resultados, dentro de un conjunto posible de soluciones, y esto aún realizando el experimento en las mismas condiciones. Por lo tanto, a priori no se conoce cual de los resultados se va a presentar:

EJEMPLO: lanzamos una moneda al aire: el resultado puede ser cara o cruz, pero no sabemos de antemano cual de ellos va a salir.

Hay experimentos que no son aleatorios y por lo tanto no se les puede aplicar las reglas de la probabilidad.

Ejemplo: en lugar de tirar la moneda al aire, directamente selccionamos la cara. Aquí no podemos hablar de probabilidades, sino que ha sido un resultado determinado por uno mismo.

Antes de calcular las probabilidades de un experimento aleaotorio hay que definir una serie de conceptos:

Suceso elemental: hace referencia a cada una de las posibles soluciones que se pueden presentar.

EJEMPLO: al lanzar una moneda al aire, los sucesos elementales son la cara y la cruz. Al lanzar un dado, los sucesos elementales son el 1, el 2, .., hasta el 6.

Suceso compuesto: es un subconjunto de sucesos elementales.

EJEMPLO: lanzamos un dado y queremos que salga un número par. El suceso "numero par" es un suceso compuesto, integrado por 3 sucesos elementales: el 2, el 4 y el 6

LECCION 12: "Regresión Lineal"

Representamos en un gráfico los pares de valores de una distribución bidimensional: la variable "x" en el eje horizontal o eje de abcisa, y la variable "y" en el eje vertical, o eje de ordenada. Vemos que la nube de puntos sigue una tendencia lineal:

El coeficiente de correlación lineal nos permite determinar si, efectivamente, existe relación entre las dos variables. Una vez que se concluye que sí existe relación, la regresión nos permite definir la recta que mejor se ajusta a esta nube de puntos.

Una recta viene definida por la siguiente fórmula:

y = a + bx

Donde "y" sería la variable dependiente, es decir, aquella que viene definida a partir de la otra variable "x" (variable independiente). Para definir la recta hay que determinar los valores de los parámetros "a" y "b":

El parámetro "a"

es el valor que toma la variable dependiente "y", cuando la variable independiente "x" vale 0, y es el punto donde la recta cruza el eje vertical.

El parámetro "b"

determina la pendiente de la recta, su grado de inclinación.

La regresión lineal nos permite calcular el valor de estos dos parámetros, definiendo la recta que mejor se ajusta a esta nube de puntos.

El parámetro "b"

Es la covarianza de las dos variables, dividida por la varianza de la variable "x".

El parámetro "a"

Es la media de la variable "y", menos la media de la variable "x" multiplicada por el parámetro "b" que hemos calculado.

EJEMPLO

LECCION 11: "Coeficiente de Correlación Lineal"

En una distribución bidimensional puede ocurrir que las dos variables guarden algún tipo de relación entre si.
Por ejemplo, si se analiza la estatura y el peso de los alumnos de una clase es muy posible que exista relación entre ambas variables: mientras más alto sea el alumno, mayor será su peso.
El coeficiente de correlación lineal mide el grado de intensidad de esta posible relación entre las variables. Este coeficiente se aplica cuando la relación que puede existir entre las varables es lineal (es decir, si representaramos en un gáfico los pares de valores de las dos variables la nube de puntos se aproximaría a una recta).

No obstante, puede que exista una relación que no sea lineal, sino exponencial, parabólica, etc. En estos casos, el coeficiente de correlación lineal mediría mal la intensidad de la relación las variables, por lo que convendría utilizar otro tipo de coeficiente más apropiado.
Para ver, por tanto, si se puede utilizar el coeficiente de correlación lineal, lo mejor es representar los pares de valores en un gráfico y ver que forma describen.
El coeficiente de correlación lineal se calcula aplicando la siguiente fórmula:

Es decir:

Numerador:

se denomina covarianza y se calcula de la siguiente manera: en cada par de valores (x,y) se multiplica la "x" menos su media, por la "y" menos su media. Se suma el resultado obtenido de todos los pares de valores y este resultado se divide por el tamaño de la muestra.

Denominador

se calcula el produto de las varianzas de "x" y de "y", y a este produto se le calcula la raíz cuadrada.

Los valores que puede tomar el coeficiente de correlación "r" son: -1 < r < 1
Si "r" > 0, la correlación lineal es positiva (si sube el valor de una variable sube el de la otra). La correlación es tanto más fuerte cuanto más se aproxime a 1.
Si "r" < 0, la correlación lineal es negativa (si sube el valor de una variable disminuye el de la otra). La correlación negativa es tanto más fuerte cuanto más se aproxime a -1.
Si "r" = 0, no existe correlación lineal entre las variables. Aunque podría existir otro tipo de correlación (parabólica, exponencial, etc.)

EJEMPLO

LECCION 10: "Distribuciones Marginales "

Al analizar una distribución bidimensional, uno puede centrar su estudio en el comportamiento de una de las variables, con independencia de como se comporta la otra. Estaríamos así en el análisis de una distribución marginal.
De cada distribución bidimensional se pueden deducir dos distribuciones marginales: una correspondiente a la variable x, y otra correspondiente a la variable y.
Distribución marginal de X

Distribución marginal de Y

EJEMPLO

LECCION 9: "Distribuciones Bidimensionales"

Las distribuciones bidimensionales son aquellas en las que se estudian al mismo tiempo dos variables de cada elemento de la población: por ejemplo: peso y altura de un grupo de estudiantes; superficie y precio de las viviendas de una ciudad; potencia y velocidad de una gama de coches deportivos.
Para representar los datos obtenidos se utiliza una tabla de correlación:

Las "x" representan una de las variables y las "y" la otra variable. En cada intersección de una valor de "x" y un valor de "y" se recoge el número de veces que dicho par de valores se ha presentado conjuntamente.

EJEMPLO

LECCIÓN 8: "Medidas de forma: Coeficiente de Curtosis"

CURTOSIS

Analiza el grado de concentración que presentan los valores alrededor de la zona central de la distribución.
Se definen 3 tipos de distribuciones según su grado de curtosis:

Distribución mesocúrtica:

presenta un grado de concentración medio alrededor de los valores centrales de la variable (el mismo que presenta una distribución normal).

Distribución leptocúrtica:

presenta un elevado grado de concentración alrededor de los valores centrales de la variable.

Distribución platicúrtica:

presenta un reducido grado de concentración alrededor de los valores centrales de la variable.

LECCION 7: "Medidas de Forma: Coeficiente de Asimetría"

ASIMETRÍA

Hemos comentado que el concepto de asimetría se refiere a si la curva que forman los valores de la serie presenta la misma forma a izquierda y derecha de un valor central (media aritemética)

Para medir el nivel de asimetría se utiliza el llamado Coeficiente de Asimetría de Fisher, que viene definido:

EJEMPLO:

LECCION 6: "Medidas de Forma: Grado de Concentración"

Las medidas de forma permiten conocer que forma tiene la curva que representa la serie de datos de la muestra. En concreto, podemos estudiar las siguientes características de la curva:

1. Concentración:mide si los valores de la variable están más o menos uniformemente repartidos a lo largo de la muestra.
2. Asimetría:mide si la curva tiene una forma simétrica, es decir, si respecto al centro de la misma (centro de simetría) los segmentos de curva que quedan a derecha e izquierda son similares.
3. Curtosis:mide si los valores de la distribución están más o menos concentrados alrededor de los valores medios de la muestra.

CONCENTRACION:

Para medir el nivel de concentración de una distribucón de frecuencia se pueden utilizar distintos indicadores, entre ellos el Indice de Gini.
Este índice se describe de mejor manera en el siguiente video:

LECCION 5: "Medidas de Dispersión "

Estudia la distribución de los valores de la serie, analizando si estos se encuentran más o menos concentrados, o más o menos dispersos.
Existen diversas medidas de dispersión, entre las más utilizadas podemos destacar las siguientes:

1. Rango: mide la amplitud de los valores de la muestra y se calcula por diferencia entre el valor más elevado y el valor más bajo.
2. Varianza: Mide la distancia existente entre los valores de la serie y la media. Se calcula como sumatorio de las difrencias al cuadrado entre cada valor y la media, multiplicadas por el número de veces que se ha repetido cada valor. El sumatorio obtenido se divide por el tamaño de la muestra.
   
   La varianza siempre será mayor que cero. Mientras más se aproxima a cero, más concentrados están los valores de la serie alrededor de la media. Por el contrario, mientras mayor sea la varianza, más dispersos están.
   
3. Desviación típica: Se calcula como raíz cuadrada de la varianza.
4. Coeficiente de varización de Pearson: se calcula como cociente entre la desviación típica y la media.

EJEMPLO

EJEMPLOS: "Medidas de Tendencia No Central"

EJEMPLO 1

EJEMPLO 2

LECCIÓN 4: "Medidas de Posicionamiento No Central"

Las medidas de posición no centrales permiten conocer otros puntos característicos de la distribución que no son los valores centrales. Entre otros indicadores, se suelen utilizar una serie de valores que dividen la muestra en tramos iguales:

• Cuartiles: son 3 valores que distribuyen la serie de datos, ordenada de forma creciente o decreciente, en cuatro tramos iguales, en los que cada uno de ellos concentra el 25% de los resultados.
• Deciles: son 9 valores que distribuyen la serie de datos, ordenada de forma creciente o decreciente, en diez tramos iguales, en los que cada uno de ellos concentra el 10% de los resultados.
• Percentiles: son 99 valores que distribuyen la serie de datos, ordenada de forma creciente o decreciente, en cien tramos iguales, en los que cada uno de ellos concentra el 1% de los resultados.

LECCION 3: "Medidas de Posición Central"

Las medidas de posición nos facilitan información sobre la serie de datos que estamos analizando. Estas medidas permiten conocer diversas características de esta serie de datos.
Las medidas de posición son de dos tipos:

• Medidas de posición central: informan sobre los valores medios de la serie de datos.
• Medidas de posición no centrales: informan de como se distribuye el resto de los valores de la serie.

MEDIDAS DE POSICION CENTRAL

1. Media: es el valor medio ponderado de la serie de datos. Se pueden calcular diversos tipos de media, siendo las más utilizadas:
   

   Media aritmética

   Se calcula multiplicando cada valor por el número de veces que se repite. La suma de todos estos productos se divide por el total de datos de la muestra

   Media geométrica

   Se eleva cada valor al número de veces que se ha repetido. Se multiplican todo estos resultados y al producto fiinal se le calcula la raíz "n" (siendo "n" el total de datos de la muestra). Según

   
   

   
   

2. Mediana: es el valor de la serie de datos que se sitúa justamente en el centro de la muestra (un 50% de valores son inferiores y otro 50% son superiores). No presentan el problema de estar influido por los valores extremos, pero en cambio no utiliza en su cálculo toda la información de la serie de datos (no pondera cada valor por el número de veces que se ha repetido).
3. Moda: es el valor que más se repite en la muestra.

LECCION 2: "Distribución de Frecuencia Absoluta y Agrupada"

La distribución de frecuencia es la representación estructurada, en forma de tabla, de toda la información que se ha recogido sobre la variable que se estudia.

• Siendo X los distintos valores que puede tomar la variable.
• Siendo n el número de veces que se repite cada valor.
• Siendo f el porcentaje que la repetición de cada valor supone sobre el total

La distribuciòn de frecuencia agrupada se agrupan los datos por intervalos, con lo que la información queda más resumida (se pierde, por tanto, algo de información), pero es más manejable e informativa
Ampliemos un poco más los conceptos en el siguiente video:

LECCION 1: "Introducción a la Estadística Descriptiva"

La estadística descriptiva es una ciencia que analiza series de datos (por ejemplo, edad de una población, altura de los estudiantes de una escuela, temperatura en los meses de verano, etc) y trata de extraer conclusiones sobre el comportamiento de estas variables.
Las variables pueden ser de dos tipos:

Variables cualitativas o atributos

Se pueden medir numéricamente (por ejemplo: nacionalidad, color de la piel, sexo).

Variables cuantitativas

Tienen valor numérico (edad, precio de un producto, ingresos anuales).

Las variables también se pueden clasificar en:

Variables unidimensionales

Sólo recogen información sobre una característica (por ejemplo: edad de los alunmos de una clase).

Variables bidimensionales

Recogen información sobre dos características de la población (por ejemplo: edad y altura de los alumnos de una clase).

Variables pluridimensionales

Recogen información sobre tres o más características (por ejemplo: edad, altura y peso de los alumnos de una clase).

Por su parte, las variables cuantitativas se pueden clasificar en discretas y continuas

1. Discretas: sólo pueden tomar valores enteros (1, 2, 8, -4, etc.). Por ejemplo: número de hermanos (puede ser 1, 2, 3....,etc, pero, por ejemplo, nunca podrá ser 3,45).
2. Continuas: pueden tomar cualquier valor real dentro de un intervalo. Por ejemplo, la velocidad de un vehículo puede ser 80,3 km/h, 94,57 km/h...etc.

Cuando se estudia el comportamiento de una variable hay que distinguir los siguientes conceptos:

• Individuo: cualquier elemento que porte información sobre el fenómeno que se estudia. Así, si estudiamos la altura de los niños de una clase, cada alumno es un individuo; si estudiamos el precio de la vivienda, cada vivienda es un individuo.
• Población: conjunto de todos los individuos (personas, objetos, animales, etc.) que porten información sobre el fenómeo que se estudia. Por ejemplo, si estudiamos el precio de la vivienda en una ciudad, la población será el total de las viviendas de dicha ciudad.
• Muestra: subconjunto que seleccionamos de la población. Así, si se estudia el precio de la vivienda de una ciudad, lo normal será no recoger información sobre todas las viviendas de la ciudad (sería una labor muy compleja), sino que se suele seleccionar un subgrupo (muestra) que se entienda que es suficientemente representativo.